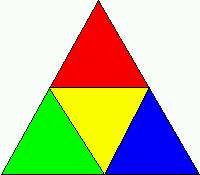

Take a piece of paper in the shape of an equilateral triangle, and cut it so that all of the pieces are also equilateral triangles. It's not possible to cut the original triangle into only two or three such pieces, but four equilateral triangles can be obtained from one without much difficulty.
What is the largest number of equilateral triangles that cannot be obtained in this way? (Assume that you may cut the triangles as small as you wish.)