The distance from the bakery to the toy store is 270 meters. (If your answer was 260 meters, did you forget the last 10 meters?)

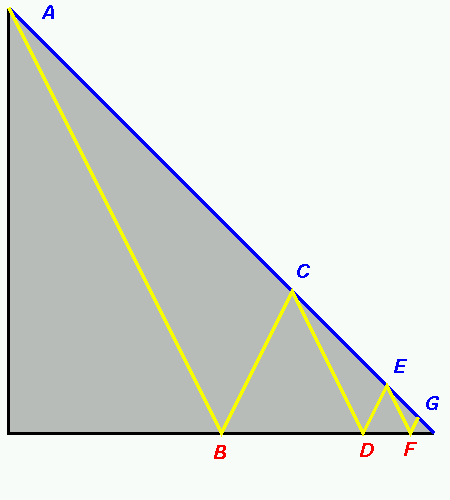
As the hints suggest, a picture helps in solving this puzzle. In this space-time graph, the vertical axis is distance (the bakery is at the top, and the toy store is at the bottom) and the horizontal axis shows time. The paths of Jeremy and his family are the yellow and blue lines. Since their speeds are constant, their paths are straight lines on the space-time graph (why?). Jeremy's higher speed means that his path appears steeper. Jeremy and his family begin at point A, and meet at points C, E, and G. Jeremy reaches the toy store at points B, D, and F. According to the information given in the puzzle, point G is 10 meters from the toy store.
To answer the puzzle, we need the (vertical) distance from point A (the bakery) to the bottom of the picture (the toy store). We can get this by determining the time intervals (measured horizontally) and the distances (measured vertically) between the points in the picture, working right to left (backwards in time).
For example, we know that the distance from F to G is 10 meters. What is the time interval from F to G? (How long does it take Jeremy to run this distance?) At 2 meters per second, it will take 5 seconds. Knowing the time interval from F to G, we can calculate how far Jeremy is from his family when he arrives at F. Since we know that they walk 1 meter per second and meet Jeremy at G five seconds later, they must be 5 meters further from Jeremy when he is at F than they are from the toy store at G, so Jeremy is 15 meters from his family when he reaches F.
Continuing to work backwards, since Jeremy runs 1 meter per second faster than his family walks, his distance from his family increases by 1 meter each second during the interval from E to F. This tells us that the time interval from E to F must be 15 seconds; adding in 5 seconds to get from F to G, the time interval from E to G is 20 seconds. Thus E is 20 meters further from the toy store than G, or 30 meters in all.
Following the same reasoning, we find that Jeremy reaches D 15 seconds before E (15 seconds times 2 meters per second = 30 meters, the distance from the toy store to E). When he reaches D he is 45 meters from his family, so he must have left C 45 seconds before reaching D. Thus C is 90 meters from the toy store, and he must have left B 45 seconds before reaching C.
We're almost back to the start! At point B, Jeremy is 90 + 45 = 135 meters from his family, so he must have run 135 seconds at 2 meters per second, or 270 meters, to get from A to B. This is the distance we needed to calculate.
You may have noticed that the distances between the successive meeting points and the toy store (270 meters, 90 meters, 30 meters, 10 meters) have the interesting property that each is 3 times as large as the next. Series such as these that grow or shrink in a constant proportion between successive terms are known as exponential or geometric series. If Jeremy were to continue to run between his family and the toy store after reaching G, where would they meet next?
Can you relate the ratio between the numbers in the series to the ratio of speeds of Jeremy and his family? (For example, what would you predict if Jeremy's speed were 3 times that of his family's walking speed?)