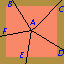
As noted in the hints for this puzzle, the solution requires that the area and the perimeter of the pie must be divided in five equal parts. Here is one way to do this:

It's easy to see that this division gives an equal amount of the outside crust to each piece; after all, that's how points C, D, E, and F were chosen. Is it possible that the pieces have equal areas, too? Remarkably, this is true.

Recall that the area of a triangle is half the product of its base and its
height (altitude). This implies that any two triangles with equal bases and
heights, such as those at right, have equal areas.
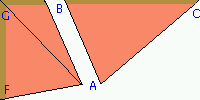 Now consider the two pieces at left, taken from the first figure above.
If the sides of the original square have a length of s, then the
area of the square is s2, and its
perimeter is 4s. The base (BC) of triangle ABC is
1/5 of this amount, or 4s/5. Since point A is at the center
of the square, the height of ABC is s/2, so its area
is
Now consider the two pieces at left, taken from the first figure above.
If the sides of the original square have a length of s, then the
area of the square is s2, and its
perimeter is 4s. The base (BC) of triangle ABC is
1/5 of this amount, or 4s/5. Since point A is at the center
of the square, the height of ABC is s/2, so its area
is
Can you show that at least one of the five pieces produced using this method, but no more than two of them, must be triangular?
The same approach can be used to divide a square pie into any number of equal pieces. In fact, this method works if the pie is in the shape of any regular polygon. Why doesn't it work for other shapes, such as rectangles?